PRINCIPIOS Y LEYES FUNDAMENTALES DE LA FÍSICA: Ley de Coulomb

Ley de Coulomb

La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia que las separa.

Esta ley es válida sólo en condiciones estacionarias, es decir, cuando no hay movimiento de las cargas o, como aproximación, el movimiento se realiza a velocidades bajas y trayectorias rectilíneas uniformes. Se le llama a esta Fuerza Electrostática.

La parte Electro proviene de qué se trata de fuerzas eléctricas y estática debido a la ausencia de movimiento de las cargas.

En términos matemáticos, la magnitud

de la fuerza que cada una de las dos cargas puntuales

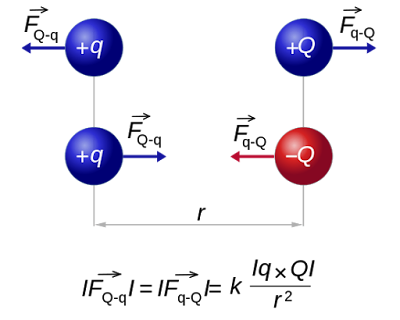
ejerce sobre la otra separadas por una distancia

se expresa como:

Ejemplo:

Las direcciones de las fuerzas sabemos coinciden con las líneas que unen a cada par de cargas puntuales. La fuerza que q1 ejerce sobre q3, F31, es de atracción. La fuerza que q2 ejerce sobre q3, F32, es de repulsión. Así, las fuerzas F31 y F32 tienen las direcciones que se indican. La separación entre q3 y q1 se obtiene de (CB)2 = (AC)2 + (AB)2 = (0.3 m)2 + (0.4 m)2, de donde CB = 0.5 m.

Las magnitudes de tales fuerzas son:

F31 = [(9x109 Nm2 /C2) (80x10-6 C) (70x10-6 C)]/ (0.5 m)2 = 201.6 N

F32 = [(9x109 Nm2 /C2) (5 0x10-6 C) (70x10-6 C)]/ (0.3 m)2 = 350 N

Conviene disponer ejes coordenados xy tal como se indica en la figura, con el origen en la carga donde deseamos calcular la fuerza resultante, en este caso en q3.

Llamando F3 a la fuerza resultante sobre q3, entonces F3= F31 + F32. Luego, en términos de componentes x e y :

F3x = F31x + F32x
F3y = F31y + F32y
F31x = F31cos